This article is available also in English.

Deconvolución Huygens

El cometido de la restauración de imágenes es averiguar lo que el instrumento intenta decirnos en realidad. — Prof. E.R. Pike, King's College, London.

Introducción

La deconvolución es una operación matemática. Se usa en restauración de señales para recuperar datos que han sido degradados por cualquier proceso físico que pueda describirse mediante la operación inversa, una convolución. Es el caso de imágenes de dispositivos ópticos como los empleados en microscopía o astronomía, pero en la práctica se aplicó primeramente a medidas sísmicas, y se extiende ya a muchos otros campos.

En microscopía, la convolución modeliza matemáticamente el proceso de formación de una imagen que sufre degradación por desenfoque y ruido. El desenfoque aparece inevitablemente en el límite de resolución del dispositivo debido a la difracción de la luz en las lentes. El ruido es normalmente "ruido fotónico", un término que se refiere a las variaciones de flujo inherentes a las propiedades estadísticas de los fotones. Puede haber otros ruidos superpuestos, pero este es inevitable, sobre todo en los límites de baja intensidad en que habitualmente se realiza la microscopía de fluorescencia.

Para caracterizar la calidad óptica de un microscopio podemos determinar cuán borrosa se vuelve la imagen de un objeto luminoso casi puntual cuando se adquiere con él. Este grado de "emborronamiento" de un simple punto es una medida de la calidad del dispositivo óptico. La imagen tridimensional que se registra de tal fuente puntual se llama función de dispersión del punto (PSF, de Point Spread Function). Las PSF desempeñan un papel básico en la teoría de formación de imágenes en un microscopio de fluorescencia.

Formación de la imagen

En sistemas incoherentes como estos microscopios (en los que la luz de distintas fuentes no produce interferencias), el proceso de formación de la imagen es lineal, y se puede describir mediante teoría de sistemas lineales. Esto significa que cuando las imágenes de dos objetos A y B se registran simultáneamente, el resultado es equivalente a la suma de sus imágenes registradas independientemente. En otras palabras: la imagen de A no se ve afectada por la de B, y viceversa.

Debido a esta propiedad de linealidad la imagen de cualquier objeto se puede "calcular" cortando el objeto en partes pequeñas, registrando sus imágenes independientemente, y después sumando todos los resultados. Cuando se divide el objeto en partes extremadamente minúsculas, en partículas puntuales de diferentes intensidades, la imagen se puede concebir como la suma de muchas PSF, cada una situada en la posición de cada partícula y ajustada su intensidad de acuerdo con la del punto correspondiente. La imagen total (borrosa) surge de la suma de todas las contribuciones de los puntos borrosos.

Resumiendo: la formación de la imagen en un microscopio de fluorescencia queda descrita por completo mediante su PSF.

Para mas información puede leer Image Formation.

Convolución

Podemos por lo tanto concebir que la imagen se forma en el microscopio reemplazando cada fuente de luz original de tamaño menor que la resolución por su PSF tridimensional (multiplicada por la intensidad correspondiente). Fijándonos sólo en una loncha XZ de una imagen 3D, el resultado se forma como sigue:

(Fig. 1)

Este proceso se describe matemáticamente con una ecuación de convolución:

$$ g\ =\ f\, \ast\, h $$ (Ec. 1)

donde la imagen g surge de la convolución de las fuentes reales de luz f (el objeto) y la PSF h. El operador de convolución * implica una integral en todo el espacio:

$$ g\ =\ f\, \ast\, h\ =\ \int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty\ f(\vec x)\ h(\vec x - \vec x')\ d^3\vec x' $$ (Eq. 2)

Interpretación

Se puede interpretar la ecuación 2 como sigue: la imagen registrada $$ g (\vec x) $$ se compone de vóxeles (ver VoXel, los equivalentes 3D de los píxeles) situados en diversas coordenadas $$ \vec x = (x,\, y,\, z) $$. La intensidad registrada en cada vóxel se debe a las distintas contribución de todos los puntos luminosos del objeto f, estando ponderadas sus intensidades por la PSF h en función de la distancia al punto considerado. Cuanto más lejos esté la fuente luminosa, menor será su contribución a la intensidad localmente registrada.

Cálculo

Esto implica que para cada vóxel situado en $$ \vec x = (x,\, y,\, z) $$ hay que calcular el solapamiento entre la función f y la PSF desplazada h. Este proceso implica calcular el valor de {$ f(\vec x)\ h(\vec x - \vec x') $} en cada punto de la imagen, y sumar todo después. Si la imagen tiene N vóxeles, el coste computacional es del orden de N².

Pero esto se puede mejorar. Un teorema importante del análisis de Fourier, el teorema de convolución, establece que las transformadas de Fourier G, F H de g, f, h respectivamente están relacionadas simplemente por una multiplicación:

$$ G = F \cdot H $$. (Ec. 3)

Esto significa que una convolución se puede calcular siguiendo estos pasos:

1. Calcular las transformadas de Fourier F yH de f y h,
2. Multiplicar F por H para obtener G, y
3. Invertir la transformación de G en g, para obtener así la imagen convuelta.

Como las transformadas de Fourier requieren un número de operaciones del orden de N log(N), este procedimiento es más eficiente que la integral previa.

Para ver cómo la aplicación de diferentes PSFs afectan a la imagen de un objeto, puede ver "the Cookie Cutter".

Deconvolución

Si la convolución implica reemplazar cada fuente luminosa puntual original por su correspondiente PSF para producir una imagen borrosa, el proceso de restauración sigue el camino inverso, recolectando toda la luz dispersa y poniéndola en su sitio de nuevo. Esto produce una mejor representación del objeto real, más clara a nuestros ojos. (El brillo de la imagen parece disminuir mientras que aumenta el contraste entre objetos y fondo, y el rango dinámico se agranda).

En términos matemáticos, la deconvolución es simplemente la resolución de la ecuación 1 mostrada más arriba, donde conocidas la imagen convuelta g y la PSF h, se obtendría la distribución de luz original f: una representación del objeto "real".

La relación de la ecuación 3 parece conducirnos a que es posible obtener la función del objeto F mediante inversión del filtro H, simplemente dividiendo F = G/H. Pero debido al carácter pasa-banda de H, esta función tiene ceros más allá de una cierta región central (ver "the Cookie Cutter"), lo que conduciría a una división entre cero de muchas frecuencias espaciales. Además, en un caso real general el ruido fotónico debe ser tenido en cuenta, así que la ecuación que en realidad debemos resolver no es la 1, sino ésta,

$$ k\ =\ f\, \ast\, h\ +\ \epsilon $$ (Ec. 4)

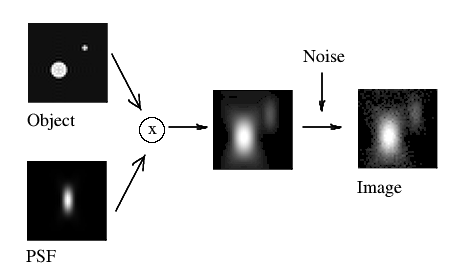(Fig. 2)

donde la imagen registrada k proviene de la convolución de las fuentes reales f y la PSF h, más el ruido fotónico ε. La división de ε entre H conduciría a una amplificación extrema del ruido y a la aparición de artefactos, debido a las regiones de H en que ésta tiene valores próximos a cero. (Por otra parte, no podemos sustraer ε de k, porque no conocemos cuál es la distribución exacta del ruido).

En conclusión, la inversión del filtro no nos permite recuperar la función del objeto real f. En vez de esto debemos encontrar una estimación de f que satisfaga algún criterio racional preestablecido, y que sea estable en presencia de ruido.

Algunos métodos de deconvolución (como la deconvolución ciega) intentan resolver la ecuación 4 sin conocer la PSF h. Aunque siempre se pueden aplicar ciertas restricciones, este procedimiento es arriesgado, porque introduce mucha indeterminación en la solución de la ecuación. Como analogía, pensemos en cuántas soluciones x, y se pueden encontrar para una ecuación algebraica como x × y = 5. Se puede hacer x tan pequeña como se desee incrementando el valor de y, y viceversa. Se puede obtener una imagen tan "limpia" como se desee, incluso totalmente vacía, haciendo la PSF más y más intensa, pero eso no implica que así se obtenga una buena representación del objeto real. La deconvolución ciega se desarrolló para imágenes astronómicas, donde la mayoría de los objetos tienen formas puntuales, lo que permite aplicar fuertes restricciones, pero hasta el momento carece de validación científica cuando se aplica a objetos complejos en microscopía.

Tenemos que buscar otra solución.

Cómo funciona Huygens

Los programas Huygens de Scientific Volume Imaging le permiten obtener una PSF de dos maneras:

• calculando una PSF teórica, obtenida de los parámetros microscópicos, un modelo del microscopio, y las ecuaciones de electromagnetismo aplicadas a la difracción, o
• "destilando" una PSF experimental a partir de medidas de calibración de cuentas fluorescentes, como se explica en Recording Beads.

El primer caso sucede automáticamente siempre que no se provea al programa de una PSF de alguna otra forma, por lo que el usuario puede proceder a la deconvolución sin preocuparse más que de describir apropiadamente el microscopio con los parámetros adecuados.

En el segundo caso, tras calcular automáticamente un modelo de la forma real de la cuenta, la PSF se calcula iterativamente de manera que su convolución con dicho modelo coincida con la imagen registrada. Esto se puede entender mejor volviendo a la figura 1 y a la ecuación 1. En este caso conocemos el objeto f (debemos saber el tamaño preciso de la cuenta esférica) y la imagen registrada g, así que podemos "destilar" la incógnita h de la ecuación.

Una vez que Huygens tiene una PSF, puede usar diferentes algoritmos matemáticos para resolver la ecuación 4 y hacer la deconvolución:

• Estimación de máxima verosimilitud clásica (Classic Maximum Likelihood Estimation)
• Estimación de máxima verosimilitud rápida (Quick Maximum Likelihood Estimation)
• Tikhonov-Miller restringido e iterativo (Iterative Constrained Tikhonov-Miller)
• Tikhonov-Miller rápido (Quick Tikhonov-Miller)

La estimación de máxima verosimilitud clásica (CMLE) es el método de restauración más versátil disponible, válido para casi todo tipo de imágenes. Se basa en la idea de optimizar iterativamente la verosimilitud de una estimación del objeto, dadas la imagen y la PSF. El objeto estimado es una imagen 3D estándar. La verosimilitud en este procedimiento se computa mediante un criterio de calidad bajo el supuesto de que el ruido fotónico está determinado por una distribución de Poisson. Por esta razón es especialmente apropiado para imágenes de baja señal, con mucho ruido fotónico. Además es muy bueno restaurando imágenes de objetos con forma puntual, lineal o plana. Ver Maximum Likelihood Estimation para más información.

En cualquier caso hay a veces situaciones en que otros algoritmos toman protagonismo, por ejemplo cuando hay que deconvolver series temporales tridimensionales, lo que requiere mucha capacidad de cálculo. En estos casos el algoritmo Quick Maximum Likelihood Estimation (QMLE) resulta mucho más rápido que el CMLE, y también proporciona excelentes resultados, sobre todo en imágenes con mucha señal y poco ruido como las de microscopios de campo ancho.

Una ventaja de emplear PSF experimentales como hacen los programas Huygens es que en esencia esto requiere del usuario que calibre su microscopio, y estimula el uso de protocolos estándar para la adquisición de imágenes. Ambas cosas aseguran el correcto funcionamiento del microscopio e incrementan enormemente la calidad y fiabilidad de los datos, y con ellas también las de los resultados de la deconvolución.

Por último, la ventaja de emplear PSF ya sea experimentales o teóricos es que permiten la programación de algoritmos muy rápidos y eficientes como el QMLE disponible en Huygens Professional o el Batch Processor. Las iteraciones en el QMLE son unas cinco veces más efectivas que las del CMLE, y se requiere menos tiempo por iteración.

Las imágenes afectadas de aberración esférica debido a un desajuste de índices de refracción se restauran mejor empleando las PSF dependientes de la posición que Huygens puede calcular automáticamente (ver Parameter Variation).

Vea cómo la deconvolución Huygens se aplica a imágenes de carácter divulgativo en Convolving Trains.

Validación

El método CMLE empleado en Huygens está respaldado por una larga lista de publicaciones científicas. Por citar algunos ejemplos (siga el enlace anterior para una lista más completa):

• Verschure P.J., van der Kraan I., Manders E.M.M. and van Driel R. Spatial relationship between transcription sites and chromosome territories. J. Cell Biology (1999) 147, 1, pp 13-24 (descargar pdf).
• Visser A.E. and Aten J.A. Chromosomes as well as chromosomal subdomains constitute distinct units in interphase nuclei. J. Cell Science (1999) 112, pp 3353-3360 (descargar pdf).
• Hell S.W., Schrader M. and Van Der Voort H.T.M. Far-Field fluorescence microscopy with three-dimensional resolution in the 100-nm Range. J. of Microscopy (1997) 187 Pt1, pp 1-7 (descargar pdf).

Ejemplos

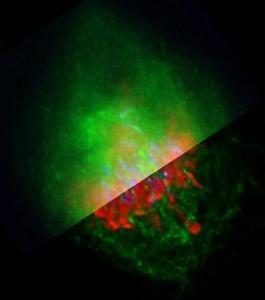
Célula humana en metafase, teñidos con marcadores fluorescentes el ADN (rojo), los centrómeros (azul) y el ciclosoma/complejo promotor de la anafase (verde). Parte superior: datos originales, Parte inferior: deconvolución con Huygens Professional. Imagen adquirida por la Dra. Claire Acquaviva, Dr. Pines Lab.

Puede encontrar más imágenes en Resolution Improvement y Evans Macrophage.

Hay un ejemplo muy sencillo y clarificador de una deconvolución hecha con el software Huygens en Decon Example. Para fines más divulgativos dispone de Convolving Trains, y de Deconvolucion En El Metro. Imágenes reales de microscopía pueden verse en la página web de SVI, en http://www.svi.nl/gallery/. Los artículos de este wiki que contienen más ejemplos están recopilados en Restoration Examples.

Más información

Vea Doing Deconvolution para más detalles, y referencias.

Nota del traductor: He adoptado el siguiente criterio: como convolución proviene del latín convolvere, lo flexiono como volver. Así, empleo convolver y deconvolver, convuelta y deconvuelta. Las alternativas frecuentemente oídas como deconvolucionar y convolucionada (o peor aún, convolvida) provienen seguramente de un abuso del participio latino convolutus que deviene un infinitivo nuevo sin demasiado fundamento. Esta decisión está, por supuesto, sometida a otra de mejor criterio, y cualquier sugerencia es bienvenida.