Excitation beam overfill factor
In confocal microscopes, the entry pupil of the microscope objective is illuminated by a laser beam. Usually, laser beams have a Gaussian profile. As a result, the illumination intensity is not constant over the pupil but will decrease towards the edges. Lower edge intensities will lower the effective NA and therefore negatively affect resolution. In most confocal microscopes this is remedied by using a beam width which is significantly larger than the entry pupil, at the cost of loss of excitation power. The ratio between the beam width and the pupil diameter is the excitation beam overfill factor and is typically in the range 1-3 for confocal exciation (2 is default). In case for STED, the laser used for depletion will usually have a lower fill factor, so that as much as possible STED power can go through the objective in order to get maximum resolution. Note that with the excitation fill factor setting in the Microscopic Parameter overview in Huygens, we refer to the excitation (confocal) fill factor only.
For some light-sheet microscopy types, it is also possible to set the excitation fill factor for the light-sheet objective(s) in Huygens. This value is typically lower than 1 to ensure a Gaussian profile of the light-sheet.
In a confocal microscope, the collimated excitation laser beam (blue) that enters the microscope objective usually overfills the back-apperture (exit pupil) of the objective before it is focussed in the sample.
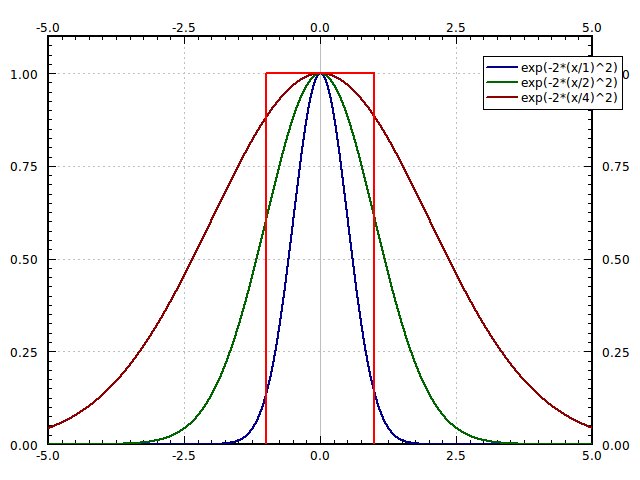
- Lens entry pupil (red), beam profile with overfill factor 1 (blue), 2 (green), and 4(dark red). At overfill factor 1 the beam edge intensity is 1/e^2 = 0.14 of the maximum, at overfill factor 2 the edge intensity is 0.61 of the maximum.
The exit pupil of your objective is decisive for the measure in which the beam expander must be used. The beam should just overfill the exit pupil. This should best be checked with every change of objective. This overfill factor (usually ranging from 2-4) can be set as a Microscopic Parameter, and is taken into account when computing a Point Spread Function (PSF) in Huygens.
For more information, see Gaussian beam in Wikipedia.
