Fourier transform
The Fourier transform (FT) is an integral transform that re-expresses a function in terms of sinusoidal functions, i.e. as a sum or integral of sinusoidal functions of different frequencies multiplied by some coefficients ("amplitudes").
Decomposing an object into spatial frequency components is called Fourier analysis; the operation which does the job is a Fourier transform. The object is in the "spatial domain", the frequency representation is in the so-called "frequency domain" or "Fourier domain" (FD).
A spatial frequency represents a (periodic) component of the object at a certain detail level. A fuzzy object will contain few high-frequency components; a fine textured object will contain many high-frequency components.
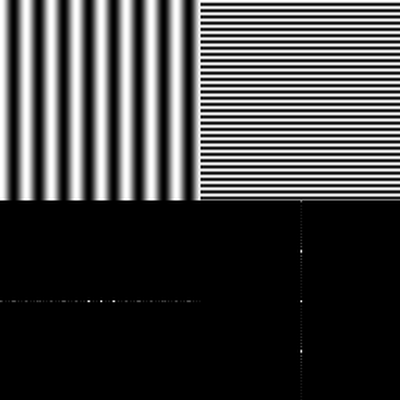
Image: Above: original object. Below: correspondent Fourier transform (amplitude). Vertical periodic structures are "horizontally periodical" (they are repeated along the horizontal direction), thus they have horizontal components in the FD. Vice versa, horizontal structures have vertical components in the FD. Here only amplitudes are represented by a grey scale, but every point in the frequency domain also has a phase that represents the displacement from the origin of the correspondent sinusoidal. (Image source with more details).
For a digitally sampled signal the discrete (or finite) Fourier transform is used, that can be efficiently calculated with the Fast Fourier Transform (FFT) algorithm. This gives information on what are the "pure" frequencies present in the signal.
One interesting property of FT's: Convolving two functions is equivalent, in the Fourier domain, to multiply their FT's (see Huygens Deconvolution).
Fourier transforms help to understand more easily many of the concepts involved in signal processing. For example, the role of a Point Spread Function as a Cookie Cutter in a Fluorescence Microscope.
See also Optical Representation.
More references:
