The Cookie Cutter

In the article about Huygens Deconvolution we explained how the image blurring in the microscope is mathematically described by a convolution equation of the form

$$ g=f \ast h $$

where the blurry image g arises from the convolution of the real light sources f (the object) and the Point Spread Function h. We also know from the convolution theorem that the Fourier Transforms G, F H of g, f, h respectively are related by simply a multiplication:

$$ G = F \cdot H $$

This means that a convolution can be computed by the following steps:

1. Compute the Fourier transforms F and H of f and h:

2. Multiply F times H to obtain G, and 3. Transform G back to g, the convolved image.

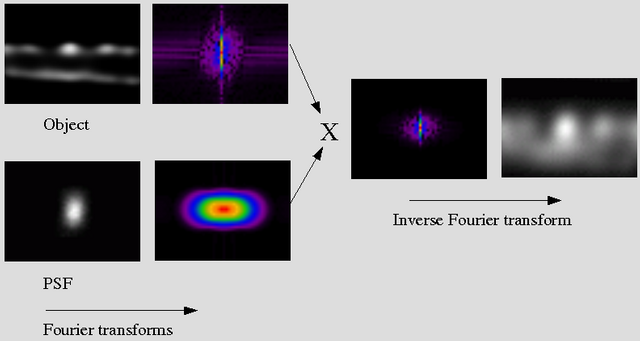
In this 2D representation you can imagine the PSF Fourier Transform (FT) working as a "cookie cutter": high-frequencies in the object FT are cut off, because of the multiplication by the zero-values of the PSF in those regions. In a 3D Image this happens in a 3D volume, of course.

This determines the Band Width of the microscope:

• Lateral around 10 cycles/micron
• Axial around 2-3 cycles/micron

In the case of a widefield microscope, the FT of the PSF (also called Optical Transfer Function) has a "missing cone" of frequencies along the Z axis. This makes all the frequencies (low and high) along this axis to be removed in the convolution process. As we mentioned in the Fourier Transform article, frequencies along a line in the Fourier domain represent structures in the perpendicular direction in the spatial domain. This missing cone of frequencies in the widefield case make all horizontal structures in the object to be missed during imaging.

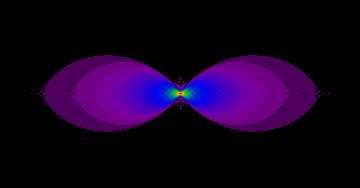Optical Transfer Function of a Wide Field Microscope.

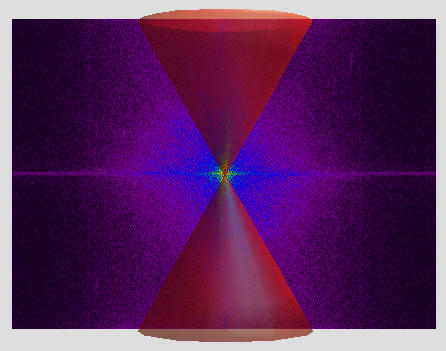The missing cone of frequencies in the widefield case.

See how this applies to an easy image in Convolving Trains.

For more info see the papers listed at the bottom page of NyquistRate