Colocalization coefficient h'
This coefficient was explained in Colocalization Theory and Colocalization Coefficients before, but is was removed from those articles because it is not reported anymore by the Huygens Software due to its difficult interpretation. Despite it involves normalized values of the pixel intensities, the coefficient itself is not normalized, and can have values larger than one. The normalization of the pixels is useful to avoid the influence of different intensity gains during the two channels acquisition, but it doesn't guarantee that the resulting coefficient is easier to interpret than the non-normalized Manders' coefficient k.
Definition
These coefficients were introducing following the reasoning at Colocalization Coefficients. To cancel out the contribution to Mander's k coefficients of an increase of signal strength in G (for example), the multiplication with G_i can be replaced by a normalized multiplication with G_i / G_max (ratio that ranges between zero and one, as G_max is the maximum of all G_i) and similarly for the R_i values:
$$ h_1' = \frac {R_{max} \sum (R_i\ G_i)} {G_{max} \sum R_i^2} $$
and
$$ h_2' = \frac {G_{max} \sum (R_i\ G_i)} {R_{max} \sum G_i^2} $$
With these modifications the colocalization of one channel with respect to the other channel can be determined independent of bleaching or sensitivity in either of the channels.
Difficult cases
The previous normalization doesn't imply that the final coefficient is easy to interpret. As an example consider the following very simple objects in channels R and G, with already normalized intensities. The green object is the simplest one: a big volume with intensity 1 against an empty background.
The red channel that we are going to consider is also very simple, but it has two different intensities. The portion of R that overlaps with the green object has homogeneous intensity r; the portion that is not colocalizing has constant intensity 1. Again the surrounding background is zero.
This could be such a thing:

In this Two Channel image only a small portion of the red object overlaps with the green object, and precisely in that portion the intensity is lower (r < 1) than in the rest of the object (1). Let's say that the overlapping volume is a and the not overlapping red volume is b.
In this simple illustrative situation the h' coefficient
$$ h_1' = \frac {R_{max} \sum (R_i\ G_i)} {G_{max} \sum R_i^2} $$
can be simplified to
$$ h_1' = \frac {\sum_a r} {\sum_a r^2\ +\ \sum_b 1^2} $$
where we have considered the sums only at the volumes a and b where the elements are non-zero. Because the intensities are homogeneous inside those volumes (in a: G_i is always one and R_i is always r; in b: R_i is always 1) the equation can be further simplified to
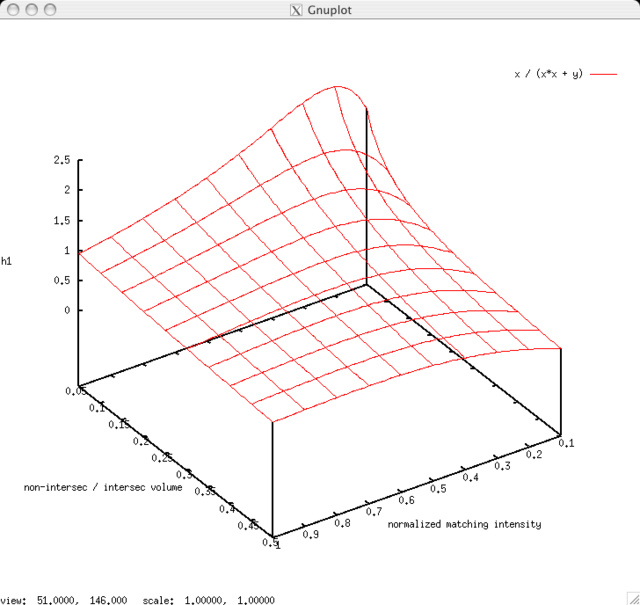
$$ h_1'\ =\ \frac {a r} {a r^2\ +\ b}\ =\ \frac {r} {r^2\ +\ b/a} $$
This quantity can indeed be larger than one when
$$ r\ -\ r^2\ >\ b/a $$
i.e., when the largest intensities in the red channel are concentrated in a relatively small non-colocalizing volume b.
To decrease the chances that this occurs, the alternative h coefficients (see below) do not normalize the pixels looking for the absolute maximum in the image but at some more stable value, precisely to avoid situations where large outliers are localized in very small regions.
In a practical situation it is unwanted that a single outlier pixel can have a major impact on the coefficients defined in this way. Because of that a more robust maximum value should be computed over a small neighborhood, smaller than the microscope's resolution. This approach is taken in the Huygens Software. The consequence of a more robust maximum is that some pixels may exceed it. To retain the property of multiplying R_i in the definition for h'_1 with a value equal or smaller that 1, G_i should be replaced by G_i,clamp so that 0 ≤ G_i,clamp / G_maxRobust ≤ 1, with G_i,clamp = G_i if G_i ≤ G_maxRobust and G_i,clamp = G_maxRobust if G_i > G_maxRobust. In this way the following more robust coefficients can be defined:
$$ h_1 = \frac {R_{maxRobust} \sum (R_i\ G_{i,clamp})} {G_{maxRobust} \sum R_i^2} $$
and
$$ h_2 = \frac {G_{maxRobust} \sum (G_i\ R_{i,clamp})} {R_{maxRobust} \sum G_i^2} $$
Still, this correction has its limitations, and if the non-colocalizing bright region of R is large enough to be considered a stable maximum, even the h coefficients can be larger than one again.
The following plot shows the values of h'_1 for different values of r and b/a: