Huygens 去卷积
The job of image restoration is to figure out what the instrument is actually trying to tell you. — Prof. E.R. Pike, King's College, London.
Table of contents
简介
去卷积，简单来说，是把一个光学显微镜特有的“卷积”现象以数学计算反推 、还原，这个计算过程是现代显微镜技术常用的处理过程，目的是把图像从成像过程中因 ”卷积” 而产生的模糊恢复过来。去卷积常用于显微镜技术与天文物理的计算，本篇会集中讨论显微镜图像的去卷积。
显微镜成像过程中，由于衍射极限 (Diffraction limit) 以及显微镜硬件的极限，成像会模糊并带噪音，噪音是由于光子通量 (photon flux) 而引起的。而成像时产生的模糊，是卷積 (Convolution) 的结果 ; 我们以一个细小的点状或小球状物体（子分辨率 Sub Resolution）来作解释 , 如果我们利用光学显微镜来采集这个小点的图像，图像采集后，我们观察到小点图像会展现出一个三维的扩散现像，就是卷积，而这个从单一子分辨率的小点的衍射出来的扩散程度，我们称为点扩散函数 (Point Spread Function, PSF)。
显微镜成像
点扩散函数 (PSF) 于光学显微镜扮演一个非常重要的角色，因为图像形成过程时，可以用一个线性的关系来表达，例如图像中的 A 点并不对 B 点有影响或干扰，B 点也不干扰 A 。因为这个线性关系，图像可以分割成更小的块，当小块是一点的话，整个图像可以描写成是由点扩散函数 (PSF) 而组成的。
卷积
我們可以想象显微镜图像可以以三维的 PSF 取代 ( PSF 乘上它们的讯号强度)，当您观察 ⅩZ 投影的话，您将观察到下图的图像形成结果：
(Fig. 1)
以数学来描述的话，将成为方程式 1 (Eq. 1)，
$$ g\ =\ f\, \ast\, h $$ (Eq. 1)
图像 g 是由光源 f （显微镜下的物体）卷积加上 PSF h。这样卷程过程也就可以以积分表达 (方程式 2, Eq. 2)。
$$ g\ =\ f\, \ast\, h\ =\ {\int\int\int}\limits_{-\infty}^\infty\ f(\vec x)\ h(\vec x - \vec x')\ d^3\vec x' $$ (Eq. 2)
去卷积
如果去卷积是卷积过程的反推或还原，这个计算结果会让我们把图像还原到与样本(或物体)本来的模样，也是说这个还原恢复后的图像比原图更能代表样本，而去卷积后的图像更清晰！而且图像的动态范围 (Dynamic range) 也增加，背景在电脑荧幕看起来较喑!
所以去卷积是解开方程1 (Eq. 1) 的答案，g 是已知数，是卷积过程后的图(采集得的图)，而 PSF h也是已知的，唯一的未知数就是 f，也就是物体本身。
由方程式 3 (Eq.3) 可以看到求 F 的话，可以利用 F = G / H，可是因为多种原因以及光子的噪音也必须考虑，所以以下方程式才是较适合使用的
$$ k\ =\ f\, \ast\, h\ +\ \epsilon $$ (Eq. 4)
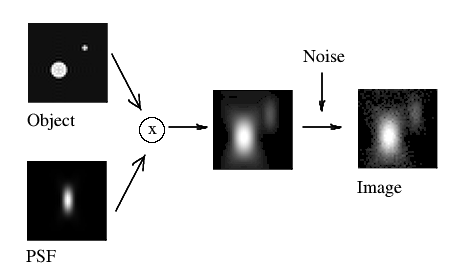(Fig. 2)
有些去卷积的计算，PSF 的 h 值并不考虑在内，例如 Blind Deconvolution，Blind Deconvolution 的计算并非一个可靠的计算方法，因为这样会引进不少可能性，例如：X * Y = 5，X 或 Y 的可能性是多于 1 个可能。所以 Huygens 的去卷积是最可靠的。
Huygens 去卷积
Huygens 去卷积是 SVI 公司研发的，用户可以选择理论 PSF 的计算或使用实验 PSF 的计算:
- Huygens 可以自动计算出 PSF 的理论值基于显微镜系统的数据，microscopic parameter 的输入或 Huygens Full File Reader 也可以直接读取显微镜厂商的文件。
- 用户可以测量莹光小球的 PSF，Huygens 可以计算出实验 PSF 再进行去卷积处理。
如果用户使用实验的 PSF，用户使用已知大小的莹光小球，方程式 1 的 PSF 并不难想象了，因为小球的大小是已知的，卷积对小球的影响，或者是小球图像因卷积而产生的扩散、模糊可以完全利用 Huygens PSF distiller 计算。
当 PSF 经过实验或理论计算后，Huygens 有以下的计算方法：
- Classic Maximum Likelihood Estimation (CMLE)
- Quick Maximum Likelihood Estimation (QMLE)
- Good's roughness Maximum Likelihood Estimation (GMLE)
- Iterative Constrained Tikhonov-Miller
- Quick Tikhonov-Miller
其中 CLME 是 Huygens 最常用、基本的恢复方法 ,对所有显微镜系统均能使用，结果能量化、比较
例子
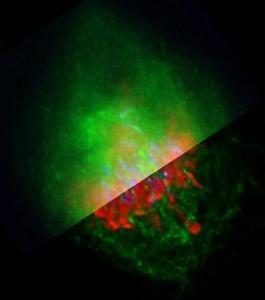A metaphase human cell stained for DNA (red), centromeres (blue) and the anaphase promoting complex/cyclosome (green).
Upper part: original data,
Lower part: deconvolved with Huygens Professional. Recorded by Dr. Claire Acquaviva, Dr. Pines Lab.
Nucleus of a human epithelium cell stained with an antibody against splicing factor.
Top part: image as restored by Huygens Professional.
Bottom part: original image.
Both parts were visualized using the Sfp Renderer. Recorded by Dr. Marjolein A. Grande.
更多的图像例子 Resolution Improvement and in Evans Macrophage.