Confocal pinhole and spatial resolution

Despite the pinhole in a Confocal Microscope does not affect the system Band Width (as explained in Pinhole And Bandwidth), it has of course a direct effect on the Spatial Resolution. The smaller the pinhole, the better the device behaves as a 3D microscope (and the lower the detected light intensity, producing lower Signal To Noise Ratios).

The size of your optical slice depends therefore on the pinhole size. Notice that the Point Spread Function (PSF) may not be zero anywhere, specially along the optical axis, and therefore giving an exact figure for the 'thickness' of the slice depends on your criterion for Spatial Resolution. In practice the Half Intensity Width of the PSF is a convenient one.

You can calculate PSF's for different pinholes (and other Microscopic Parameters) using the online Nyquist Calculator and checking the box that says 'Calculate also PSF'. Here we show three different PSF's for standard confocal conditions, with increasing Back Projected Pinhole Radius (BPPR).

These are top view (XY) Maximum Intensity Projections (MIP) in false color representation. The green color represents an intensity about the half of the red maximum.

The same, now with lateral (XZ) views:

Notice that doubling the pinhole at each step indeed reduces the resolution. Each PSF (the image of a single point) is larger than the previous one. But not twice as large.

In the XY plane the difference in size of the green ring (HIW) is not much noticeable (the diameter is always about seven pixels, ~ 300 nm), thus you may be tempted to say that resolution is not worsened. Still, the blur beyond that point goes to a much larger extent on the second and third images. Adjacent points would be less differentiable during imaging, and contrast is compromised.

This also shows that any definition of Spatial Resolution to characterize your setup, apart from being arbitrary, may not exactly represent what you need. (That's why, to define the Ideal Sampling, the less arbitrary Band Width criterion is used).

Along the optical axis Z (vertical in the XZ views) the enlargement of the HIW is slightly more noticeable (from about 6 pixels, or 780 nm, to more than 7 pixels, or 910 nm): resolution is always worsened more along the optical axis.

Common parameters: The 3D images dimensions are 1.74x1.74x5.73 microns. Each VoXel is 43x43x130 nm (Nyquist Rate), thus you can easily calculate the side of the green rings in X, Y and Z by counting image 'pixels' and multiplying by the correspondent dimension.

• Microscope type: confocal
• Numerical aperture: 1.4
• Excitation wavelength: 488 nm
• Emission wavelength: 520 nm
• Number of excitation photons: 1
• Lens medium refractive index: 1.515
• Specimen medium refractive index: 1.45
• Acquisition depth: 0 (at the coverslip)

Images generated by the Nyquist Calculator.

HIW resolution as function of the pinhole for various objects

So far we've been discussing the resolution of a confocal system for point objects. However, point-resolution is not always relevant, for example when imaging sheet-like objects like cell membranes. Especially the resolution for horizontal plane-like objects is very much dependent on the pinhole size. The following graph illustrates this point (FWHM = HIW).



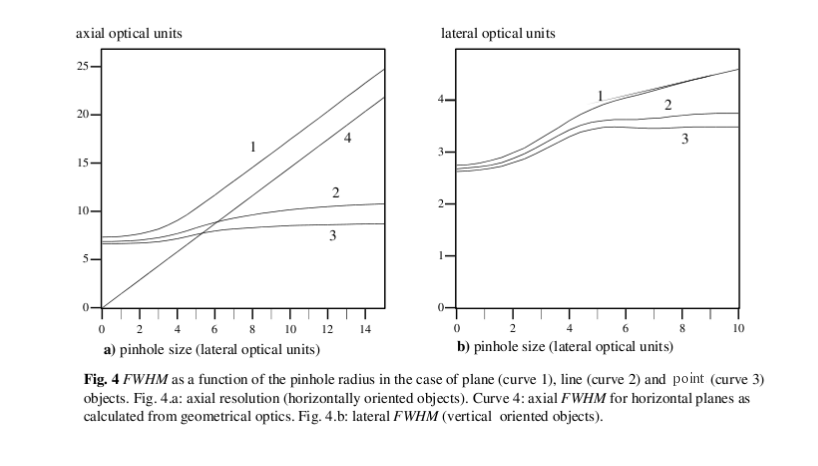
Dimensions are in Optical Units. Note how the Z-resolution for horizontal planar objects (curve 1) keeps linearly decreasing with increasing pinhole size, whereas for point and line objects resolution doesn't decrease anymore for larger pinholes.

Optical slice thickness

Clearly the qualitative concept of 'optical slice thickness' is related to resolution. It is clear from the graph above that it is also related to the content of the 'slice'. Assuming the 'slice' contains plane like objects, 'optical slice thickness' will be strongly dependent on the pinhole size. On the other hand, if a 'slice' contains a few sparse point objects or filaments, 'optical slice thickness' will not so much affected by large pinholes.

For more details, see 3-D image formation in high-aperture fluorescence confocal microscopy: a numerical analysis, H. van der Voort and G. Brakenhoff, J. of Microscopy, 158(1), 43-54 (1990).