ナイキストレート (The Nyquist rate)

基本

この記事の前に、サンプリング密度を読むことをお勧めします。

ここで重要な点は、画像取得時の理想的なサンプリング密度は、顕微鏡の光学系に依存するということです。点像分布関数（PSF）は、画像が「構築」される基本的な「ブリック」であるため、利用可能なすべての情報を収集するには、少なくとも PSF のスケールで詳細を記録する必要があります。デコンボリューションは、PSF スケールで動作する操作であり、画像取得がより大きなスケールで行われる場合、画像復元は、役に立たない可能性があります。品質対サンプリングを参照してください。

ナイキスト計算アプリと計算機

Android デバイス用の Nyquist アプリのバージョンについては、このページにアクセスしてください。 また、無料で使用できる Nyquist Calculator をオンラインで提供しています。

序論

Nyquist-Shannon サンプリング定理は、「シグナルをサンプリングする時に（例えば、アナログシグナルからデジタルに変換するとき）、サンプリングされたバージョンから元のシグナルを完全に再構築できるようにするために、サンプリング周波数は、入力シグナルの帯域幅の 2 倍よりも大きくなければならない」と定めています。（Whittaker と Shannon の両方の出版物を参照してください； 以下の参照リストを参照してください）。

ナイキスト基準は、顕微鏡からのすべての情報を画像に取り込むために必要な最小サンプリング密度を決定します（結像を参照）。 サンプリング距離がナイキスト距離よりも大きい場合、画像に関する情報は失われます。 このアンダーサンプリング状態は、エイリアシングアーティファクトも発生させます。エイリアシングアーティファクトは、ギザギザのエッジ（階段状）または、フリンジとして現れる場合があります。 これらを画像から除去するのは非常に困難です。

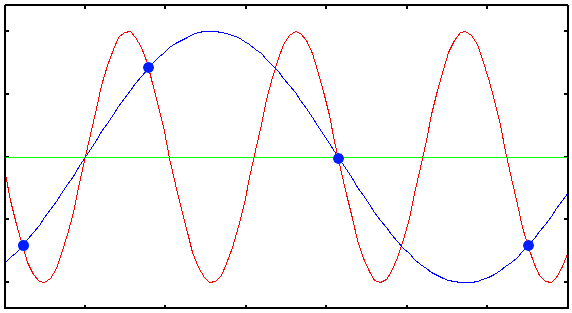
1D 正弦波シグナルのサンプリング不足の取得を示すプロット。 青色の点は、赤色のシグナルを記録するために取得されたデジタルサンプルです。 明らかに、元のシグナルを再構築するのに十分ではありません。 それらから補間できるのは、青色の間違ったシグナルだけです。

画像情報コンテンツの観点からは、オーバーサンプリング、つまりナイキスト距離よりも短い間隔でのサンプリングは、計算時間とストレージ要件が高くなることを除けば害はありません。それでも、オーバーサンプリングは、必要以上に取得時間が長くなる可能性があり、そのため、例えば、褪色効果が発生する可能性があります。 多くの場合、サンプリング密度、ライン平均化、レーザー強度、および取得時間の間で妥協点を見つけることができます。

空間解像度の観点から理想的なサンプリングを定義することは、経験則として（「レイリー基準の半分のサンプル」）頻繁に行われますが、これは、正確には正しくなく、場合によっては、アンダーサンプリングにつながります（例えば、ピンホールと帯域幅を参照してください）。 理想的なサンプリングレートは、点像分布関数によって決定されるシステムの帯域幅に関してより適切に定義されます。

サンプリング密度

顕微鏡の光学系によって生成されたすべての情報がデジタル形式で取得されることは、デコンボリューション結果の品質にとって非常に重要です。サンプリング密度が特定の値よりも高い場合、対象物に関するすべての情報が取得されることを示すことができます。 この値をクリティカルサンプリング距離と呼び、ナイキストレートに対応します。 褪色、画像取得時間、データサイズなどの実際的な問題は別として、逆にクリティカル距離よりも小さいサンプリング距離（オーバーサンプリング）を使用することに異論はありません。

次の図は、特定の波長に対する対物レンズの開口数（NA）に対するこの重要なサンプリング距離の依存性を示しています。 これらの曲線を異なる波長に適用するには、縦軸を波長でスケーリングするだけです。 例： NA 1.3、蛍光波長 570 nm の広視野顕微鏡（WF）を使用しています。 プロットから、500nm 蛍光での重要な横方向ナイキストサンプリング距離は、95 nm であることがわかります。 この場合、これは、570/500 × 95 nm = 108 nm になります。

上の曲線は、広視野およびコンフォーカル顕微鏡の軸方向および横方向のクリティカルサンプリング距離を示しています。 どちらの場合も蛍光波長は、500 nm です。

コンフォーカルの場合、ナイキストサンプル距離を決定するのは励起波長です。 理論上、ピンホール半径は、何の役割も果たしませんが、大きなピンホールは、解像度の限界で微細構造を大幅に減衰させます。 したがって、経験則として、一般的なピンホールの直径が 1 エアリーディスクの場合、横方向のクリティカルサンプリング距離は、50 % 増加する可能性があり、情報の損失は無視できます。ピンホールがはるかに大きい場合、横方向のイメージング特性は、広視野（WF）システムの特性に非常に似ており、それに応じてサンプリング距離を設定できます。 軸方向のサンプリング距離が大幅にクリティカル距離を超えて大きくすることはお勧めしません。

計算

	ナイキスト計算機を使用すると、光学条件に応じて、画像の取得に使用する理想的なサンプ
リング密度を見つけることができます。

方程式

上記のプロットは、さまざまな NA にもかかわらず 1.51 の固定屈折率を想定しているため、軸方向のサンプリングの向きを示しているだけです。 そのプロットを作成するために使用される詳細な方程式は次のとおりです。

広視野の場合

従来の蛍光広視野顕微鏡のナイキストクリティカルサンプリング距離は、次の式で与えられます：

$$\Delta_x=\frac{\lambda_{em}}{4 n \sin(\alpha)}$$ $$\Delta_z=\frac{\lambda_{em}}{2 n (1-\cos(\alpha))}$$ (式 1)

n は、レンズ屈折率（通常は、油浸の場合は、1.515）、 α は、対物レンズの半開口角、 𝜆 𝑒𝑚 は、蛍光波長、 ∆x 、 ∆z は、それぞれ横方向と軸方向のサンプリング距離です。 これは、顕微鏡の解像度の約半分です。（広視野顕微鏡のサンプリングは、励起波長に依存しないことに注意してください。）

上記の式では、 α は、次の式から計算できます：

$$\alpha=\arcsin(\text{NA}/n)$$ (式 2)

開口数 NA を使用します。（式 2）から、開口数とレンズ屈折率の関係がわかります。

$$\text{NA}=n\sin(\alpha)$$ (式 3)

sin(𝛼) は、常に 1 より小さいので、NA は、常に n より小さいことがわかります。

パラメータリストで NA を 1.2 に設定し、屈折率を 1.2 以下に設定すると、Huygens ソフトウェアは、-+"Warning: total reflection at glass/medium interface, setting G_alpha to pi/2"+- を表示し、理論 PSF を生成しようとします。

1.3 N.A. の油浸対物レンズの場合、 α は、約 1.0 ラジアンで、60 度に近くなります。

ナイキストレートと帯域幅

上記の ∆x 値と、 ∆z 値は、距離であり、システムを通過する最高空間周波数の周期長の半分に対応します。したがって、ナイキストレート（単位距離あたりのサイクル数）は、次のようになります：

$$F_{\text{Nyquist},x}=\frac{1}{2\Delta_x}$$ $$F_{\text{Nyquist},z}=\frac{1}{2\Delta_z}$$

これは、多くの場合、システム帯域幅と呼ばれます。

コンフォーカルの場合

コンフォーカル顕微鏡の場合、従来の広視野顕微鏡の上述のサンプリング距離は、2 で割る必要があります。

コンフォーカルの場合、点像分布関数（PSF）の合計は、独立した励起点像分布関数と検出点像分布関数の積です。 励起と蛍光の波長は、ほぼ等しく、有限サイズの検出ピンホールのぼやけ効果は、検出システムの帯域幅を変更しないため、PSF 全体の帯域幅は、2 倍になります。 システム帯域幅がこのように 2 倍になるため、コンフォーカルナイキストサンプリング距離は、同等の広視野サンプリング距離の半分になります。

$$\Delta_x=\frac{\lambda_{ex}}{8 n \sin(\alpha)}$$ $$\Delta_z=\frac{\lambda_{ex}}{4 n (1-\cos(\alpha))}$$ (式 4)

コンフォーカルサンプリング距離を計算するには、励起波長 𝜆 𝑒𝑥 を使用する必要があります。

帯域幅が 2 倍になったからといって、解像度が 2 倍になるわけではありません。少なくとも、解像度にレイリー基準を使用していないからです。 実際、この基準では、横方向の解像度は約 1.4 倍しか改善されません。 帯域幅が 2 倍になることは、空間的にもコントラストの向上に反映されます。

コンフォーカル顕微鏡は、広視野顕微鏡の 2 倍の細部を伝達できますが、残念ながら、これらは、非常に大きく減衰します。 最高周波数の 60 % を超えると、特に、理想的ではないピンホールの場合、実質的に何も伝達されません。 したがって、理論上のナイキストサンプリングレートを使用すれば、ほとんど問題はありません。 しかし、理論的なレートの 60 % で実用的なナイキストレートを使用することは正当です（50 / 0.6 = 80 nm あたり約 1 サンプル）。

広視野の場合、高空間周波数も限界に近づくにつれて減衰しますが、コンフォーカルの場合よりもはるかに少ない程度です。 したがって、広視野画像をアンダーサンプリングにしないことをお勧めします。

マルチフォトンの場合

k フォトン励起のマルチフォトン顕微鏡の場合、励起点像分布関数は、k 乗されるため、理論上の帯域幅は、k 倍になります。 しかし、これは、励起波長の拡大によって補償されます。これは、単一フォトンの場合と比較して、約 k 倍になります。 また、帯域幅の制限が大幅に緩和されます。

その結果、ピンホールが大きい場合または、ピンホールがない場合の適切なサンプリングレート（情報ページの Huygens で 2 フォトンデータを処理する方法を参照してください）は、実際の励起波長をフォトン数 k で割った値で上記の広視野の場合と同じ方程式を使用することで得られます：

$$\Delta_x=\frac{\lambda_{ex}}{4 k n \sin(\alpha)}$$ $$\Delta_z=\frac{\lambda_{ex}}{2 k n (1-\cos(\alpha))}$$ (式 5)

重要なことは、帯域通過ボリュームの 3D 形状が非常に異なることです： 広視野領域の中心には、くさびがあり、大きな広視野ぼやけ円錐が生じますが、マルチフォトン帯域通過ボリュームには、そのような欠陥はありません。

典型的な例

したがって、励起波長が 480 - 520 nm の一般的なコンフォーカル顕微鏡と 1.3 NA の対物レンズは、横方向のサンプリング距離 50 nm、軸方向のサンプリング距離 150 nm でサンプリングする必要があります。 経験豊富なコンフォーカル顕微鏡オペレーターは、このような小さなサンプリング距離が褪色効果を引き起こすことに異議を唱えるかもしれません。 これは、より粗くサンプリングされた画像と同じ見かけの S/N 比を達成しようとする場合に当てはまります。 ただし、復元手順により、見かけの S/N 比が劇的に改善されます!!! したがって、高密度にサンプリングされた画像は、通常よりもシグナル／ノイズが低くなる可能性があります。 実際には、平均化回数をサンプリング距離と交換できます。 例えば、標本の同じボリュームから 4 倍以上でサンプリングされた場合、平均カウントは、同じ係数だけ減らすことができます。

さらに読むための提案

Gonzalez による「デジタル画像処理」の画像サンプリングと量子化に関するセクション（セクション 2.3） を参照してください； このトピックの詳細については、Woods（ISBN 0201180758）までお問い合わせください。

このページで使用されている方程式の参照先は次のとおりです：

• Wilson, T. and Tan J.B. Three dimensional image reconstruction in conventional and confocal microscopy. (1993) BioImaging 1:176-184.
• Sheppard, C.J.R., A. Choudhury and J. Gannaway. Electromagnetic field near the focus of wide-angular lens and mirror systems. IEE J. (1977) Microwaves, Opt. Acoust. 1, 129-132.
• Sheppard, C.J.R. The spatial frequency cut-off in three-dimensional imaging. (1986a). Optik 72 No. 4 131-133.
• Sheppard, C.J.R.The spatial frequency cut-off in three-dimensional imaging II. (1986b). Optik 74 No. 3, pp. 128-129.

サンプリング定理に関する参考文献は次のとおりです：

• Whittaker E.T., On the functions which are represented by expansions of the interpolation theory (1915). Proc. Roy. Soc. Edinburgh Sect. A, 25:181.
• Shannon C.E., Communications in the presence of noise. (1949) Proc. IRE, 37:10
• Goodman J.W. Introduction to fourier optics 2nd ed. (1986) McGraw-Hill Book Companies Inc.