---

Distorted colocalization

It is assumed that noise is the largest source of experimental trouble when measuring CoLocalization (for example by means of the Pearson's correlation coefficient PPC), lowering the measured value away from the real one. In this article we will illustrate that the blurring implicit in the Image Formation (and completely described by the Point Spread Function PSF) may be as much a disturbing problem as noise, but in the opposite direction, depending on the scale of our analysis. Other acquistion factors affecting colocalization analysis such as chromatic aberration and channel crosstalk (bleedthrough) can be corrected with Huygens Chromatic Aberration and CrossTalk & Autofluorescence Corrector, respectively. These will not be further discussed here.
The key idea is that colocalization depends on the resolution of the experiment. Basically, we have to define at what level we consider things to be "at the same place". Obviously, at the molecular level things never overlap. At a planetary scale, any two objects inside the same cell nucleus can be considered to be colocalizing.

In any case (independently of what practical volume of interest we define) the colocalization analysis is limited by the resolution of our acquisition devices. When two objects are separated in a distance smaller than our experimental resolution, they will always look as colocalizing. And this has (almost) nothing to do with having a very high number of pixels in our camera or with using a high confocal zoom: the Spatial Resolution is limited by the Image Formation process in the lenses, and can't be improved by arbitrarily recording more and more pixels.

Therefore if your volume of interest is of a size comparable to the size of the PSF or smaller (in a regular Confocal Microscope this is a little spheroid of about 700 nm in diameter along the optical axis) it doesn't matter if your pixels are as small as 50 nm: things inside the PSF range will look as colocalizing even if they are not at the pixel scale.

There are some experimental and mathematical tricks to reduce the influence of noise in the measurements, and it is usually considered that methods like DeConvolution are too computationally demanding and not really necessary for this purpose. That would be the case if only noise were involved. Different experimental techniques improve the localization of particles (PALM) or image interaction between molecules of certain types and not their mere presence on a voxel (FRET). But to reduce the effect of the blurring in a given image there is no other trick, only deconvolution is an option. And because it is such an important source of error (when the volume of interest is comparable to the PSF) it should be considered carefully.

Simulated experiment

We will show the influence of blurring by using a very simple test image. We made a small synthetic image with sparse pixels in the red and the green channels, distributed in a pattern all over the 3D volume. The image is 52 pixels large in all three dimensions, and the non-zero pixels are concentrated in the inner 32 x 32 x 32 pixels volume to leave some empty border around them. Still the image is not a cube in space, because the Sampling Density is anisotropic: each VoXel is 50 x 50 x 170 nm large. In real life, there could be many fluorescent molecules inside each of this illuminated voxels, but this is a typical Nyquist Rate for a regular Confocal Microscope.

As it is generated, this image represents a distribution of molecules that do not colocalize at all. Fluorescent red and green pixels are all set to a value of 200 in a 8 bit image. No red pixel coincides with any green one, and they are even in separate XY planes. This is a top view Maximum Intensity Projection (MIP) of it:



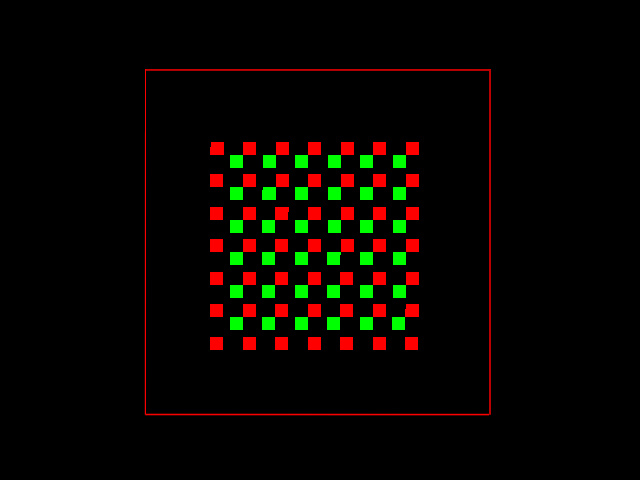
And this is a perspective Simulated Fluorescence Process rendering (SFP) of this simple test image:




Using Huygens' Colocalization Analyzer we find that the PPC of this distribution is almost zero (-0.002).

Just adding Photon Noise to such an image won't change the results. The PPC remains zero.

But such a distribution of molecules would never be imaged like that in a fluorescence microscope, which always adds blur during the Image Formation. We can easily simulate the image acquisition convolving that original dye distribution with the PSF of a confocal microscope (objective with Numerical Aperture 1.3, Emission Wavelength of 520 nm, Back Projected Pinhole Radius of 250 nm). This is again a MIP top view of the result:



And this a perspective SFP rendering:



The fluorescent intensities are now so spread all over the volume that they colocalize noticeably!!! The same analysis now provides a PPC of 0.767. This simulated image is still noise free: adding Photon Noise to the image (Signal To Noise Ratio = 10) provides this other result:



The PPC is slightly reduced to 0.744. Therefore the noise indeed decreases the colocalization parameter... respect to the blurred image, not to the real molecule distribution!

Any correction method applied to the final image could maybe recover the noise free PPC value of 0.767, but that is not the colocalization of the real molecule distribution at the original scale of interest, that was almost zero.

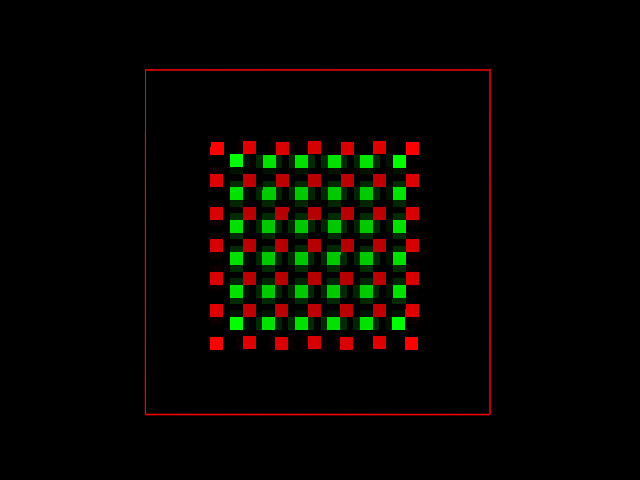
We can now try to deconvolve both simulated images, with and without noise, and see what can be recovered from the real distribution. After fifty iterations of the Quick Maximum Likelihood Estimation (QMLE) restoration method, the noise free image provided the following result, with a PPC of -.004.



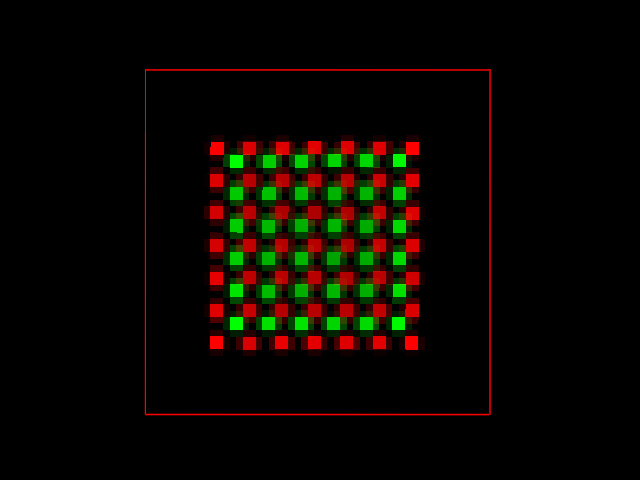
Applying the same algorithm to the noisy image the result was not so perfect, but the PPC still provides a more realistic value of -0.005.

Conclusion

During the image acquisition many experimental factors alter the measurement of the real distribution of molecules, which affects any further analysis. Because the colocalization parametrization requires defining at what scale we consider it, blurring may be a practical problem if our scale of interest is smaller than the typical blurring distance. Of course, if your scale of interest for colocalization study is larger than about 500 nm, then the blurring may even be beneficial for the analysis, and deconvolution will only help you in reducing the noise levels. In these simulations, deconvolution proved to be a beneficial method to revert the imaging distortions (not only noise, but also blur) and recover a more realistic distribution of the original object at the pixel scale on a Nyquist Rate sampled image. In particular, the very much affected PPC colocalization parameter provided realistic results only after deconvolution.