Huygens デコンボリューション: 顕微鏡画像の復元

「画像復元の仕事は、装置が実際に何を伝えようとしているのかを理解することです」
-- E.R. Pike 教授、キングスカレッジ、ロンドン。Table of contents
はじめに
デコンボリューションは、逆の操作である畳み込みによって説明できる物理プロセスによって劣化した画像を復元するために、画像復元で使用される数学的操作です。 これは、顕微鏡や天文学で使用される光学システムによる結像の場合だけでなく、地震測定の場合にも当てはまります。
顕微鏡では、この畳み込みプロセスが、ぼやけとノイズによって劣化した画像の形成を数学的に説明します。 ぼやけは、主に機器による回折限界のイメージングによるものです。 ノイズは、通常、フォトンノイズであり、入射フォトン束の固有の自然変動を指す用語です。
単一の点のような(サブ解像度)対象物の広がり(ぼやけ)の程度は、光学システムの品質の尺度です。このような単一の点光源のぼやけた 3D 画像は、通常、点像分布関数(PSF)と呼ばれます。
結像
PSF は、蛍光顕微鏡の結像理論において重要な役割を果たします。 この理由は、蛍光顕微鏡などのインコヒーレントイメージングシステムでは、結像プロセスが線形であり、線形システム理論によって記述されるためです。 これは、2 つの対象物 A と B が同時にイメージングされる場合、結果は、個別にイメージングされた対象物の合計に等しいことを意味します。 言い換えると、 A のイメージングは、 B のイメージングの影響を受けず、その逆も同様です。
線形特性の結果として、任意の対象物の画像は、対象物を部分に分割し、これらのそれぞれを画像化し、その後、結果を合計することによって計算できます。 対象物を非常に小さな部分、つまり、さまざまな高さの点対象物に切り刻むと、画像は、PSF の合計として計算され、それぞれがその位置に移動され、対応する点の強度に従ってスケーリングされます。 結論として、蛍光顕微鏡でのイメージングは、その PSF によって完全に記述されます。
詳細については、結像を参照してください。
畳み込み
元のすべてのサブ解像度光源をその 3D PSF(対応する強度を掛けた値)に置き換えることによって、顕微鏡で画像が形成されると想像できます。 3D 画像の 1 つの XZ 断面だけを見ると、結果は次のようになります:
 (図. 1)
(図. 1)
このプロセスは、次の形式の畳み込み方程式によって数学的に記述されます。
$$ g\ =\ f\, \ast\, h $$ (式. 1)
ここで、画像 g は、実際の光源 f (対象物) と PSF h の畳み込みから生じます。 畳み込み演算子 *は、空間全体の積分を意味します:
$$ g = f \ast h = \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty} f(\vec{x}') h(\vec{x} - \vec{x}')\ d^3\vec{x}' $$ (式. 2)
解釈
式 2 は、次のように解釈できます: 位置にあるボクセルで記録された強度
$$ \vec x = (x,\, y,\, z) $$ 画像の g(𝑥) は、対象物 f のすべてのポイントの寄与から生じます。それらの実際の強度は、考慮されるポイントまでの距離に応じて PSF h によって重み付けされます。
計算
つまり、位置する各ボクセルに対して $$ \vec x = (x,\, y,\, z) $$ 目的関数 f と(移動した) PSF h の間のオーバーラップを計算する必要があります。 このオーバーラップの計算には、画像全体の \( f(\vec x)\ h(\vec x - \vec x') \) の値の計算と合計が含まれます。 画像全体に N 個のボクセルがあるため、計算コストは、 N2 のオーダーになります。
しかし、これは改善することができます。 フーリエ理論の重要な定理である畳み込み定理は、 g、 f、 h のそれぞれのフーリエ変換 G、F、H が単純な乗算によって関連付けられると述べています。
$$ G = F \cdot H $$. (式. 3)
これは、畳み込みを次の手順で計算できることを意味します:
- f と h のフーリエ変換 F と H を計算
- F に H を掛けて G を得る
- G を畳み込み画像 g に変換
フーリエ変換は、N log(N) のオーダーで多くの操作を必要とするため、これは前の積分よりも効率的です。
さまざまな PSF の適用が対象物のイメージングにどのように影響するかを確認するには、Cookie Cutter をお読みください。
デコンボリューション
畳み込みが、すべての元の(サブ解像度)光源を対応する PSF に置き換えてぼやけた画像を生成することを意味する場合、復元手順は、逆の方法に進み、この拡散光をすべて収集して元の位置に戻します。これにより、実際の対象物がよりよく表現され、私たちの目には、より明確になります。(これにより、画像のダイナミックレンジが増加し、バックグラウンド領域が暗くなります!!!)。
数学的に言えば、デコンボリューションは、上記の式. 1 を解くだけです。 ここで、畳み込み画像 g と PSF h がわかっている場合は、元の光分布 f を取得します: これは、「実際の」対象物の表現です。
式. 3 の関係は、単に F = G/H を除算するだけで、逆フィルター処理によって、目的関数 F を取得できることを暗示しているように思われます。 しかし、H の帯域制限特性により、特定の領域の外側にゼロがあり(Cookie Cutter を参照)、多くの空間周波数でゼロによる除算が発生します。 また、実際の一般的な場合では、フォトンノイズを考慮に入れる必要があるため、実際に解かなければならない方程式は、式. 1 ではありません、しかし これは:
$$ k\ =\ f\, \ast\, h\ +\ \epsilon $$ (式. 4)
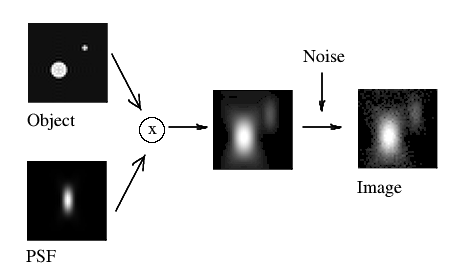 (図. 2)
(図. 2)
ここで、取得された画像 k は、実際の光源 f と PSF h とフォトンノイズ ε の畳み込みから生じます。ε を H で除算すると、極端なノイズ増幅が発生し、帯域内の H の値が小さい領域が大きいため、膨大なアーティファクトが発生します。(また、正確なノイズ分布が何であるかを知ることができないため、k から ε を単純に差し引くことはできません)。
したがって、逆フィルタリングでは、真の目的関数 f を復元することはできません。 代わりに、適切な基準を満たし、ノイズの存在下で安定している推定 f' を見つけようとする必要があります。
一部のデコンボリューション手法(ブラインドデコンボリューションなど)は、PSF 項 h を知らなくても式. 4 を解こうとします。 いくつかの制約を適用できますが、方程式の解に多くの不確定性が導入されるため、これは、常に危険です。(x × y = 5 の形式の代数方程式に対して x、y の解をいくつ見つけることができますか?) これらの方法を顕微鏡に適用した場合、現在、科学的な検証が欠けています。
別の解決策に行かなければなりません。
Huygens デコンボリューション ソフトウェアの仕組み
Scientific Volume Imaging 社の Huygens ソフトウェアを使用すると、次の 2 つの方法で PSF を取得できます。
2 番目の場合では、ビーズ形状のモデルが与えられた場合、ビーズモデルとの畳み込みが測定されたビーズ画像と一致する PSF が「抽出」されて計算されます。 これは、図 1 と式 1 を振り返って理解できます。 これで、対象物 f がどのようなものであるかがわかり(球状ビーズの正確なサイズがわかっている必要があります)、その画像 g を取得したので、方程式で残りの未知の項 h を抽出できます。
PSF が提供されると、Huygens は、さまざまな数学的アルゴリズムを使用して畳み込み方程式 4 を効果的に解き、デコンボリューションを実行できます。
- Classic Maximum Likelihood Estimation
- Quick Maximum Likelihood Estimation
- Iterative Constrained Tikhonov-Miller
- Quick Tikhonov-Miller
- Good's Roughness Maximum Likelihood Estimation
Classic Maximum Likelihood Estimation(CMLE)は、利用可能な最も一般的な復元方法であり、ほぼすべての種類の画像に有効です。 これは、測定された画像と PSF に基づいて、対象物の推定値の可能性を繰り返し最適化するという考えに基づいています。 対象物の推定は、通常の 3D 画像の形式です。この手順の見込みは、フォトンノイズがポアソン統計によって管理されるという仮定の下で、品質基準によって計算されます。 (検出器によって収集された光電子は、ポアソン分布を示し、シグナルとノイズの間に平方根の関係があります)。 このため、低シグナル画像に最適です。 さらに、点、線、または平面のような対象物の画像を復元するのにも適しています。 詳細については、Maximum Likelihood Estimation を参照してください。
ただし、計算負荷が非常に高い 3D タイムシリーズをデコンボリューションする場合など、他のアルゴリズムが優先される状況もあります。 この場合、CMLE-time よりもはるかに高速で優れた結果が得られる Quick Maximum Likelihood Estimation-time(QMLE)の使用を検討できます。 Good's roughness Maximum Likelihood Estimation アルゴリズム(GMLE)を使用すると、非常にノイズの多い画像、特に STED およびコンフォーカルデータの処理が改善されます。
Huygens のように測定された PSF を使用する利点は、本質的に、顕微鏡を校正する必要があり、イメージングのための標準プロトコルの使用を促進することです。 これらを組み合わせることで、顕微鏡の正しい機能が保証され、顕微鏡データ自体の品質と信頼性が大幅に向上し、デコンボリューション結果の品質と信頼性も大幅に向上します。
最後に、理論的または測定された PSF の利点は、Huygens Essential と Professional、および Workflow Processor にある QMLE のような非常に高速なアルゴリズムの構築を容易にすることです。 QMLE での反復は、CMLE 反復よりも約 5 倍効果的であり、反復ごとに必要な時間が短くなります。
屈折率の不一致による球面収差の影響を受ける画像は、深さ依存の PSF を使用することで、Huygens ソフトウェアでより適切に復元されます(パラメータの変動を参照)。
通常、Huygens アルゴリズムは強度保存を行います。
Convolving Trains の一部のアクセス可能な画像に Huygens 復元が適用されていることを確認してください。
検証
Huygens で使用される CMLE 法は、かなりの科学文献によって裏付けられています。 ここでは、関連する例を 3 つだけ挙げます(より長いリストについては、前のリンクをたどってください)。
- Verschure P.J., van der Kraan I., Manders E.M.M. and van Driel R. Spatial relationship between transcription sites and chromosome territories. J. Cell Biology (1999) 147, 1, pp 13-24 (get pdf).
- Visser A.E. and Aten J.A. Chromosomes as well as chromosomal subdomains constitute distinct units in interphase nuclei. J. Cell Science (1999) 112, pp 3353-3360 (get pdf).
- Hell S.W., Schrader M. and Van Der Voort H.T.M. Far-Field fluorescence microscopy with three-dimensional resolution in the 100-nm Range. J. of Microscopy (1997) 187 Pt1, pp 1-7 (get pdf).
例
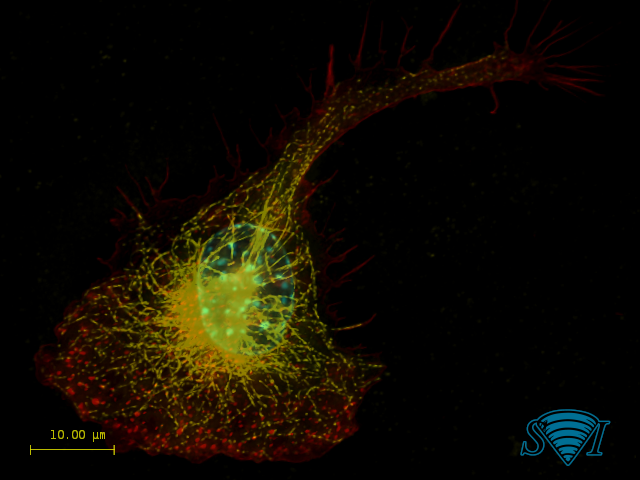
実験的な点像分布関数は、落射蛍光顕微鏡で赤色、緑色、および青色のチャネルに対して生成され、ミトコンドリア(赤色)、F-アクチン(緑色)、核(青色)。 デコンボリューション前(左図)とデコンボリューション後(右図)の画像を並べてマージし、デコンボリューションの威力を示しました。 米国、NIH、NIEHS の Jeff Tucker 博士と Holly Rutledge 博士が作成した画像。
詳細情報
特別なトピックとリファレンスについては、デコンボリューションの実行を参照してください。
Huygens デコンボリューションのテスト
Huygens ソフトウェアは、当社のウェブサイトから無料でダウンロードできます。 Huygens ソフトウェアをインストールして起動した後、一時的なテストライセンスをリクエストして、Huygens のデコンボリューション、ビジュアリゼーションおよび復元オプションを調べることができます。 すべての製品を無料でお試しください。 ソフトウェアには、ライセンスなしで実行できる多くのフリーウェアツールもあります。
参考文献
AII amacrine cells: quantitative reconstruction and morphometric analysis of electrophysiologically identified cells in live rat retinal slices imaged with multi-photon excitation microscopy. Brains Structure & Function 1–32 (2016) このホワイトペーパーでは、適用された最適なイメージングとデコンボリューション設定について詳しく説明します。
Correlated confocal and super-resolution imaging by VividSTORM. Nature Protocols 11, 163–183 (2016) Huygens デコンボリューションは Nature Protocols の今号の表紙を作成するために使用されました。
Viruses 2018, 10(1), 28; doi:10.3390/v10010028 デコンボリューションには Huygens を使用しました。
詳細については、ここをクリックしてください。
